Vapour and Gas
Vapour is the evaporated phase of a liquid with some liquid in suspension. Gas is the vapour phase of a liquid above the critical temperature. Vapour is a partially evaporated stage of a liquid. But, in case of a gas the evaporation is fully completed. The behaviour of a vapour is not exactly the same as that of a gas. We will discuss the gas law that are obeyed by perfect or ideal gases.
Ideal or Perfect Gas
An ideal or perfect gas obeys the gas laws under all conditions of temperature and pressure. Having said that, for all practical purposes, gases are considered ideal or perfect gas if they behave quite accurately within some preselected region of temperature and pressure. No real gas obeys gas laws perfectly. Gases like nitrogen, oxygen, air, dry and superheated steam etc. are assumed to be ideal or perfect gas in thermodynamic analysis.
Boyle’s Law
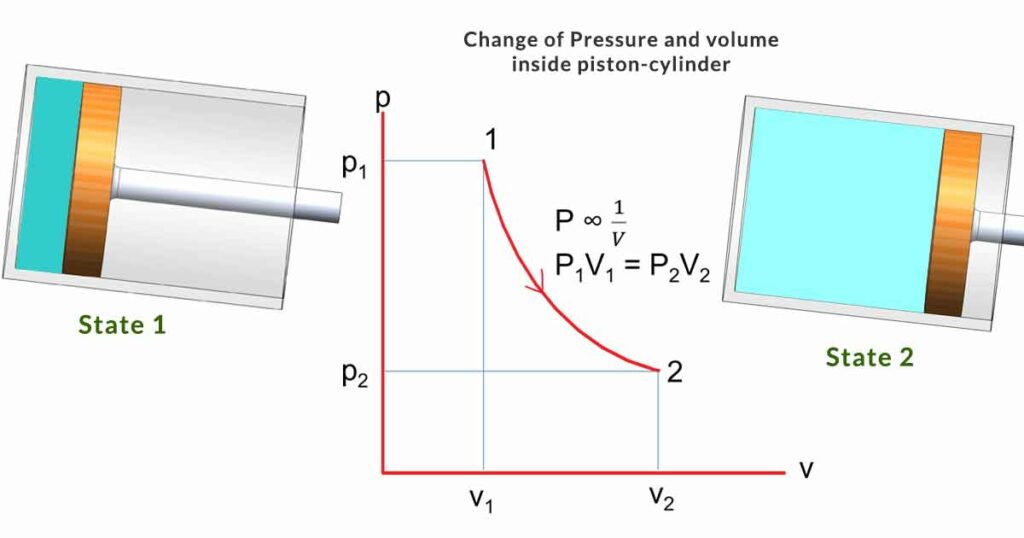
It is an experimental gas law that describes how the pressure of a gas changes with the volume of the container if mass and temperature are kept constant (Closed system; isothermal process). Statement:
The absolute pressure of a given mass of an ideal gas is inversely proportional to the volume if the temperature and amount of gas remain unchanged within a closed system. Mathematically,
P ∞ 1/V
Or PV = constant (k)
For a change of state from state 1 to state 2
P1V1 = P2V2
The figure with piston-cylinder arrangement shows two states (state 1 and state 2) with p-v diagram. The gas inside the cylinder expands from state 1 to state 2. Pressure decreases and volume increases.
Charles’ Law
Charles’s law is an experimental gas law which describes how volume of a mass of gas changes when temperature increases and pressure is kept constant (Closed system, isobaric process).
Statement of the Charle’s Law:
When the pressure of a given mass of an ideal gas is constant, Volume is directly proportional to the absolute temperature. Mathematically,
V ∞ T, if p is constant.
V = kT
V/T = k
V1/T1 = V2/T2
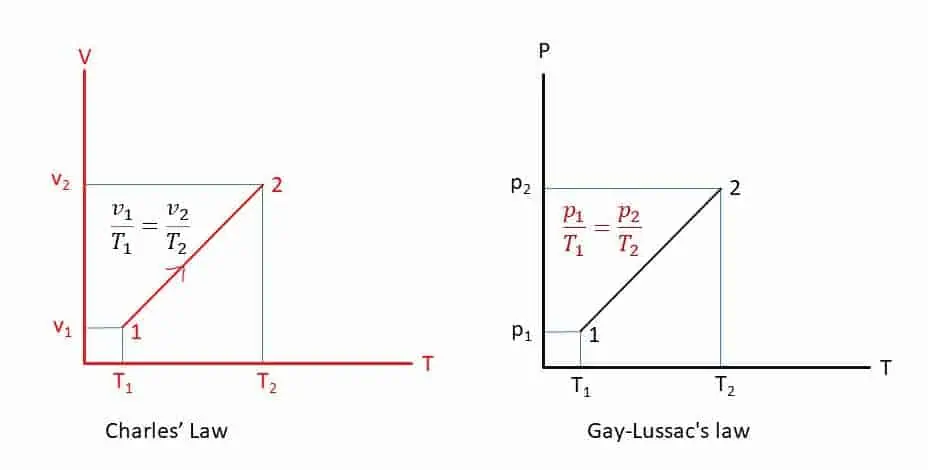
Gay-Lussac’s law
The pressure of a given mass of gas is directly proportional to the absolute temperature of the gas if the volume is kept constant. This law is commonly known as the Pressure Law or Amontons’s law and Dalton’s law. Mathematically,
P ∞ T if V is constant.
P = kT
P/T = k
P1/T1 = P2/T2
Characteristic Gas Equation (Gas Law)
If we Combine both Boyle’s and Charles’ laws for a unit mass of a perfect gas,
P ∞ 1/v if T is kept constant (Boyle’s Law)
Or v ∞ 1/p if T is constant and
v ∞ T if p is kept constant (Charles’ Law)
We get, pv/T = constant (v is specific volume v = V/m )
p1v1/T1 = p2v2/T2 = Constant = R
The constant R is specific for a particular gas. Or value of R is different for different gas. We can say R is the characteristic of a specific gasTherefore, ‘R’ is called Characteristic gas constant or Specific Gas constant (R). The value of R for atmospheric air is approximately 0.287 kJ/kg K. The characteristic gas equation is
Pv = RT
If m kg of gas is considered,
PV = mRT (v = V/m)
Universal Gas Equation
The value of universal gas constant (Ru) is same for any perfect gas. Ru = 8.314 kJ/kg-mole K.
Ru = M. R where M = molecular mass or molar mass.
Molecular mass is a number equal to the sum of the atomic masses of the atoms in a molecule. For example, molecular mass of Oxygen (O2) is 16. And therefore, Characteristic gas constant (R) of O2 is 8.314/32 = 0.2598 kJ/kg K.
If we write the characteristic gas constant in terms of molar mass the equation is known as Universal gas equation.
PV = nRuT where n = No of kg mole.
Avogadro’s law
The volume (V) of a gas is proportional to the number of moles (n) of an ideal gas if the temperature and pressure are kept constant. Mathematical,
V ∞ n
V = kn
Watch this video on Gas Law
Specific Heat of a gas
Gases have two specific heats: specific heat at constant volume and at constant pressure.
Specific heat at Constant volume (cv)
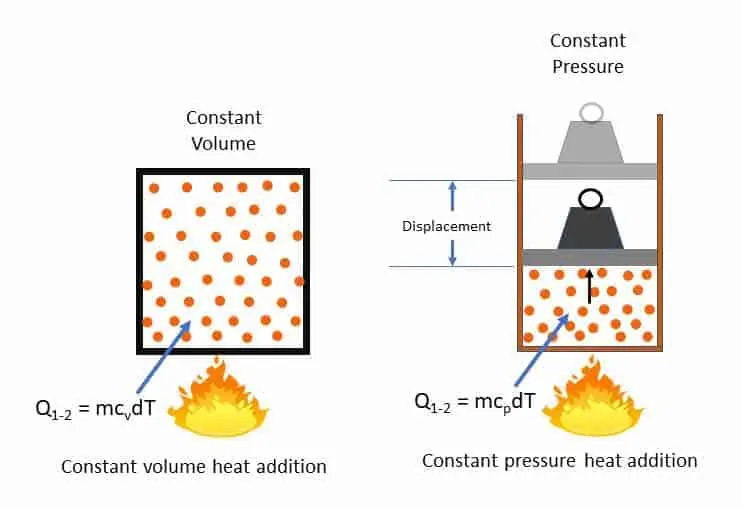
It is the amount of heat to be added to raise the temperature of the gas by one degree by keeping the volume constant (kJ/kg K). The total amount of heat (Q1-2) to be added to m kg of gas in a closed vessel to increase the temperature from T1 to T2 degree is
Q1-2 = m cv (T2 – T1) {kg. (kJ/kg k). K}
= mcvdT kJ
Fom the figure below you can visualise that no displacement of boundary is there. No displacement work is done by the system. Internal energy of the system will increase due to increase in temperature.
Specific heat at Constant Pressure (cp)
It is the amount of heat to be added to raise the temperature of the gas by one degree by keeping the pressure constant (kJ/kg K). The total amount of heat (Q1-2) to be added to m kg of gas at a constant pressure to increase the temperature from T1 to T2 degree is
Q1-2 = m cp (T2 – T1) {kg. (kJ/kg k). K}
= mcpdT kJ
From the second diagram below, you can notice some displacement work is done due to heat addition to the system at constant pressure. In addition to work done the intenal energy (U) will also increase due to temperature rise.
Video on Specific Heat
Enthalpy (H)
Enthalpy is one of the properties of a thermodynamic system. We will discuss enthalpy in more detail in the coming posts. It is a state variable or a point function. Enthalpy is combination of other point functions. It is the sum of internal energy and product of pressure and volume. Mathematically,
H = U + PV
Specific enthalpy, h = u + pv
Enthalpy is generally expressed as change in enthalpy (∆H or dH) for a process between two states.
∆H = ∆U + ∆PV
For a constant pressure process,
∆H = ∆U + P∆V
= Q1-2 (from first law of thermodynamics)
In our upcoming post we will discuss Zeroth Law and First Law of Thermodynamics.
Questions and Answers
1 Which thermodynamic process is represented by Boyle’s Law?
Answer: Boyle’s Law represents isothermal or constant temperature process. Boyle’s Law describes the relation between Volume and pressure if temperature is kept constant (isothermal).
2. What is hyperbolic process in thermodynamics?
Answer: In hyperbolic process, the product of pressure and volume remain constant (PV = constant). Hyperbolic process is governed by Boyle’s Law. It also represents isothermal process.
3. Under what conditions general gas law becomes Boyle’s law or Charles’ law?
Answer: The general gas law can be written as
If temperature remain constant (T1 = T2), the gas law becomes
P1v1 = p2v2, Boyle’s Law. → p ∞ 1/v
Again, If pressure remain constant (isobaric, p1 = p2), the gas law reduces to Charles’ law.
V1/T1 = V2/T2 → v ∞ T