Second Law of Thermodynamics

Introduction

We have discussed about the limitations of first law of thermodynamic in one of our previous posts. We have also discussed about applications of First law to non-flow processes. First law does not indicate the direction in which the heat and work flow and it does not mention any condition under which these interactions take place. First law states that both heat and work are mutually convertible. Although mechanical work can be fully converted to heat, only a part of the heat can be converted to mechanical work

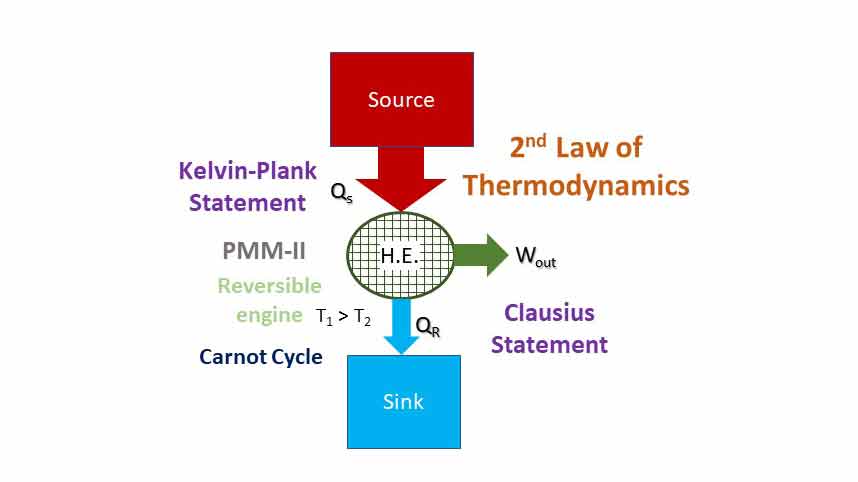
There are many statements of Second law of thermodynamics. These statements give answers to questions of directionality and provide some concepts. For example, Clausius gave an important inequality principle-the concept of entropy, the law of increase in entropy for the universe, and the concept of energy. Second law states that whole of heat energy cannot be converted to mechanical energy and a part of the heat must be rejected to the surrounding. Second Law of thermodynamics is, therefore, popularly known as law of degradation of energy.

Important Terms

Thermal energy reservoir:

This is a hypothetical body with very large heat capacity that can supply or absorb finite amount of heat without any change in its own temperature.

Source:

A thermal reservoir which supplies heat energy is called a source.

Sink:

A thermal reservoir that absorbs heat energy is known as a sink.

Heat Engine:

Devices which convert heat energy into mechanical work are called Heat Engines. They receive heat from a source at high temperature and convert part of it into work. The rest of the heat is rejected to the Sink at low temperature.

Heat engines operate on a cycle. They generally involve a fluid called working fluid to and from which heat is transferred during the cycle. The figure shows a heat engine with heat input of Q_s from a source and heat rejected Q_r to a sink. For a closed system, work output or net work done W_out = Q_s – Q_r.

Thermal Efficiency (η_th) of Heat Engine:

The measure of performance of a heat engine is its thermal efficiency. Thermal efficiency is the ratio of net work output to the heat input.

$Thermal\ efficiency=\frac{Net\ work\ output}{Total\ heat\ supplied}$

$\eta_{\left(th\right)}=\frac{W_{\left(out\right)}}{Q_s}=\frac{Q_s-Q_r}{Q_s}=1-\frac{Q_r}{Q_s}$

Heat Pump:

Heat Pump is a device (thermodynamic system) which receive heat from a body at low temperature and supply heat to a body (Room) at higher temperature by using external energy in the form of work input. It can be considered as a reversed heat engine. Figure below explains the principle of a heat pump.

Q₂ quantity of heat is received from a body at low temperature T₂ and Q₁ quantity of heat is supplied to a body (room) at high temperature T₁. Mechanical work W_p is consumed or used as work input by the system of heat pump. The desired effect of a heat pump is to supply heat to the room to maintain at higher temperature than the surrounding.

Co-efficient of Performance of Heat Pump (COP_HP):

The performance of a heat pump is measured by Coefficient of Performance (C.O.P.). C.O.P. of a heat pump is defined as the ratio of heat supplied (Q₁) to the work input of heat pump (W_p). C.O.P. of a heat pump is also known as Energy Performance Ratio (EPR). Heat pump is used to keep a room warm than the surrounding.

$\left(COP\right)_{\left(HP\right)}=\frac{Heat\ supplied}{Work\ Input}=\frac{Q_1}{W_p}=\frac{Q_1}{Q_1-Q_2}\ \left(since\ Q_1=Q_2+W_p\right)$

$\left(COP\right)_{\left(HP\right)}=\frac{T_1}{T_1-T_2}$

Refrigerator:

Refrigerator is also a Heat pump. A refrigeration is used to maintain a space at lower temperature than the atmosphere by extracting heat at low temperature and rejecting the heat to atmosphere at high temperature at the cost of compressor work input. Figure below represents the principle of a refrigerator.

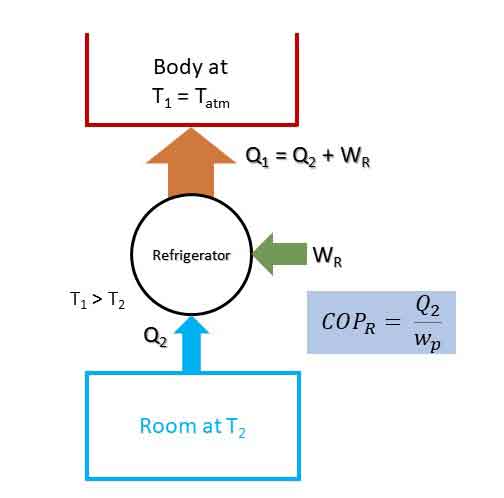
Co-efficient of Performance of Refrigerator (COP_R):

$\left(COP\right)_R=\frac{Heat\ extracted\ from\ Refrigerator}{Work\ supplied\ or\ work\ input}$

$=\frac{Q_2}{W_R}$

$=\frac{Q_2}{Q_1-Q_2}$

$=\frac{T_2}{T_1-T_2}$

$=\frac{\left(T_1-T_2\right)-T_1}{T_1-T_2}$

$=1-\frac{T_1}{T_1-T_2}$

$COP_R=1-COP_{\left(HP\right)}$

$\left(COP\right)_{\left(HP\right)}=1+\left(COP\right)_R$

Statements of Second Law of Thermodynamics

Although many statements of Second Law of Thermodynamics are available, we will discuss two main statements of the law: Kelvin-Plank Statement and Clausius Statement.

Kelvin-Plank Statement

“It is impossible to construct an engine working in cyclic process whose sole effect is the conversion of all the heat energy supplied to it by the source into an equivalent amount of work.”

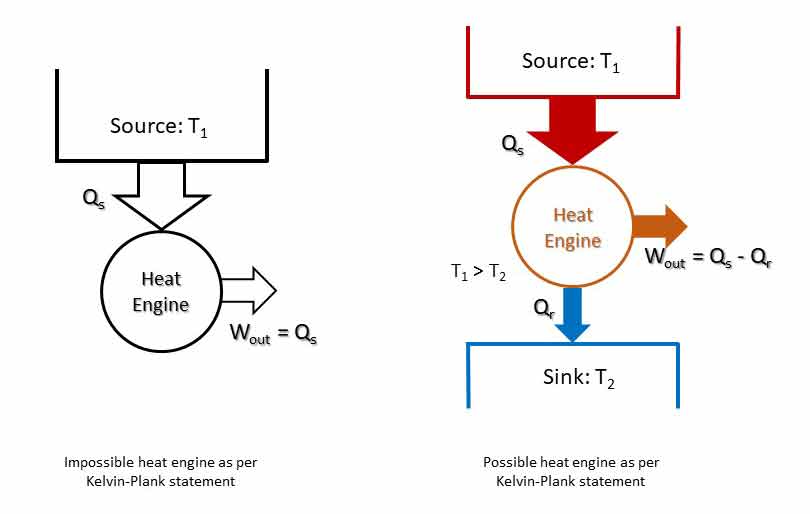
Thus, it says that heat cannot be completely converted to work. Or the efficiency of an engine cannot be 100%.

In a cyclic system, energy cannot be stored in the system. If all the heat cannot be converted to work and no energy can be stored, some of the energy received must be rejected. The difference between heat supplied and work done (Q_s – W_out = Q_R) must be rejected to a sink at lower temperature. Such a device is shown which is in line with Kelvin-Plank statement.

Clausius Statement

“It is impossible for energy in the form of heat to flow from a body at lower temperature (sink) to a body at higher temperature (source) without the aid of external work.”

“It is impossible to construct a device working in a cyclic process whose sole effect is the transfer of energy in the form of heat from a body at lower temperature (sink) to a body at higher temperature (source) without the aid of an external agency.”

Thus, it states that external work (input) is required to pump heat from a sink to a source (Heat pump or Refrigerator).

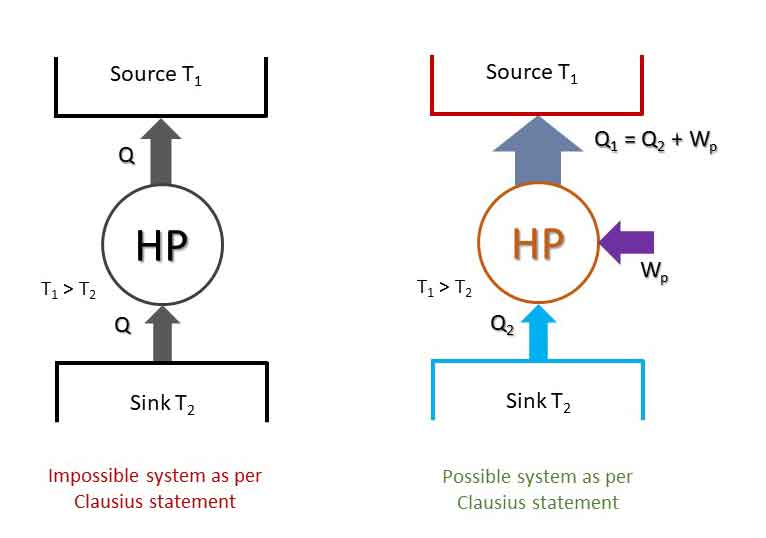
The impossible system and possible systems as stated by Clausius statement are shown in the figure. Although Kelvin-Plank and Clausius statements looks different at the first sight, in fact, they are equivalent in all respect. Both the statements say the same thing. If a system violates kelvin-Plank statement, it also violates the Clausius statement. It can be proved.

Perpetual Motion Machine of Second Kind (PMM-2)

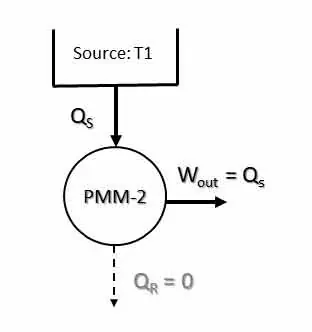
Perpetual Motion Machine of Second Kind is a machine or device which violates the second law of thermodynamics. A heat engine which converts whole of the heat energy into mechanical work (100% efficiency) is called PMM-2. In other words, a PMM-2 is an engine working in cyclic process whose sole effect is the conversion of all the heat energy supplied to it by the source into an equivalent amount of work. PMM-2 is a fictitious machine or device that gives net work in a complete cycle by exchanging heat with a single reservoir. Thus, it violates the Kelvin-Plank statement of the second law of thermodynamics. Figure below shows a PMM-2 that delivers work output while exchanging heat with a single reservoir (source).

Carnot Cycle

In 1824, Sadi Carnot proposed a hypothetical working cycle for heat engine with highest possible efficiency. An engine that works on this cycle is called Carnot engine. Carnot engine is an idealised engine for comparing performance of other practical heat engine. Carnot cycle consists of two reversible isothermal processes and two reversible adiabatic processes. Carnot assumed an ideal cylinder with perfect insulated wall and piston. He also assumed that the head of the cylinder is perfect heat conductor for heat transfer. The cylinder contains air and air is assumed as perfect gas. The processes and steps of the cycle are, shown in the figure below. The cylinder head can be insulated by a cap after the heat transfer.

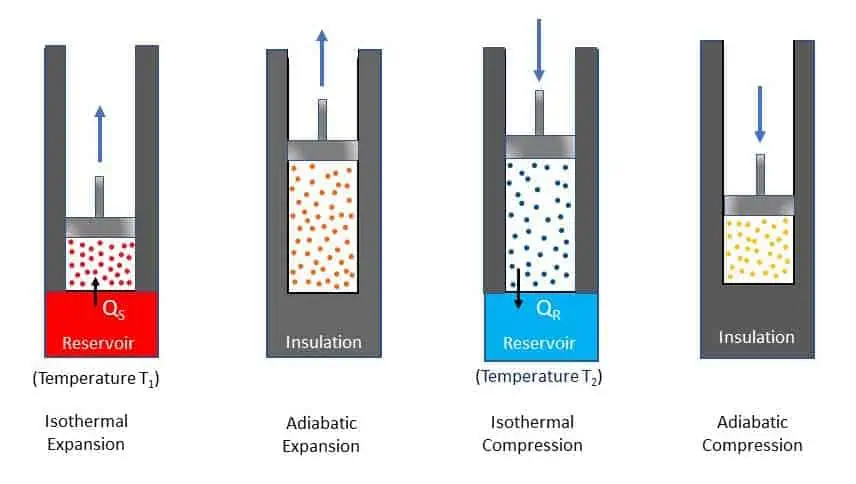
Figure below represents Carnot engine cycle in a p-v diagram. The four processes of the cycle are:

Isothermal Expansion 1-2: The piston moves very slowly from state 1 to state 2 while the cylinder head is in contact with source at temperature T₁. Thus, Q_S quantity of heat is transferred to air at constant temperature T₁ during the process 1-2 and volume changes from v₁ to v₂.
Adiabatic Expansion 2-3: After removing the source, perfect insulator is brought in contact for complete insulation (no heat transfer) and allowed to expand further at very high speed. Because of the expansion, the temperature falls from T₁ to T₂.
Isothermal Compression 3-4: The sink at temperature T₂ comes in contact with the cylinder head. During the compression from volume v₃ to v₄, Q_R quantity of heat is rejected to the sink isothermally at constant temperature T₂.
Adiabatic Compression process 4-1: The gas is again insulated thermally while compression takes place from v₄ to v₁. Since the compression is adiabatic, the temperature rises from T₂ to T₁ again and the cycle is completed.

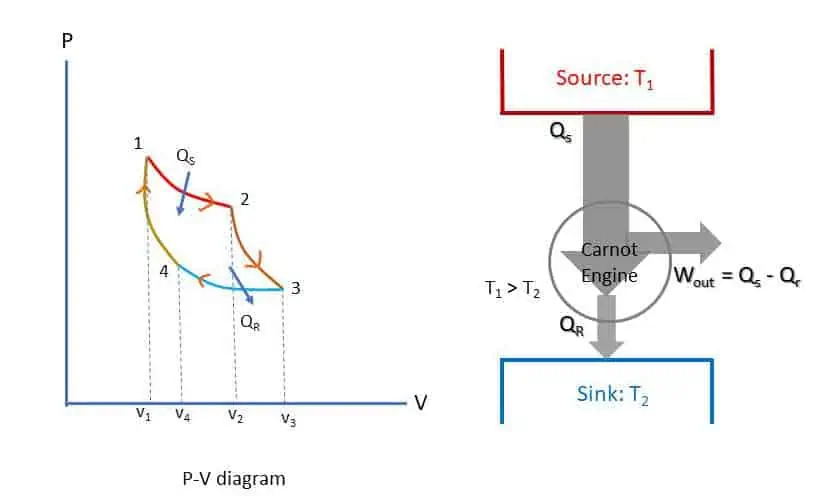
There is no mass flow throughout the cycle. The area of the cycle is equal to the work done by the cycle. Heat Q_S is supplied to the system during the process 1-2 and heat Q_R is rejected during the process 3-4. Therefore, work output of the cycle is Q_S – Q_R. The efficiency of the cycle is

$\eta=\frac{Work\ output}{Heat\ input}$

$\eta=\frac{Q_S-Q_R}{Q_S}=1-\frac{Q_R}{Q_S}$

Thus, efficiency is 100% if heat rejected to the sink is 0. But as per Second Law of thermodynamics, heat engine cannot work without rejecting some amount of heat to the sink.

Carnot principles

The thermal efficiency of an irreversible heat engine is always less than the thermal efficiency of a reversible heat engine working between same two reservoir.
The thermal efficiency of all reversible heat engine working between two same reservoirs are same.

Therefore, the thermal efficiency of reversible heat engine is function of temperature only.

Carnot engine efficiency

$\eta_{\left(th,\ rev\right)}=f\left(T_1,\ T_2\right)$

$Therefore,\ \frac{Q_S}{Q_R}=f\left(T_1,\ T_2\right)$

$Or,\ \left(\frac{Q_S}{Q_R}\right)_{\left(rev\right)}=\frac{T_1}{T_2}$

$Therefore,\ \eta_{\left(carnot\right)}=1-\frac{Q_R}{Q_S}=1-\frac{T_2}{T_1}$

The thermal efficiency of a heat engine can be increased by supplying the heat from the source to the engine at maximum possible temperature and rejecting the heat to the sink at minimum possible temperature.

Second Law of Thermodynamics

Introduction