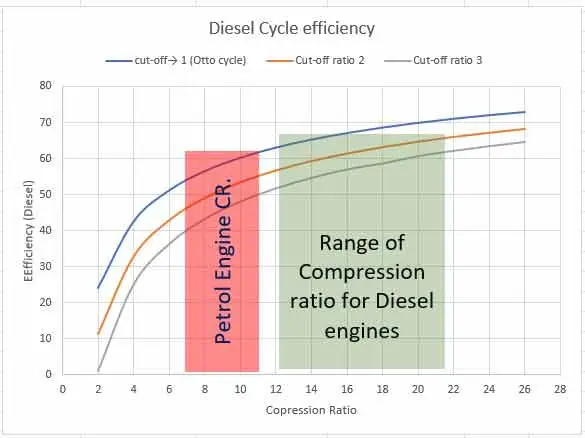
Introduction

We have discussed the mass and energy transfer in a thermodynamic system. We have also defined thermodynamic process and system property. In an open system mass interaction takes place between system and its surrounding. Energy transfer can happen in both open and closed system.

Energy

It is capacity to do work. It may exist in many forms. Energy within the system boundary is known as stored energy. Examples of stored energy are potential energy, kinetic energy, internal energy etc. Energy that in the process of crossing the system boundary is called energy in transition or transit. Examples Heat, work etc. Heat transferred may be designated as thermal energy and work done may manifest as mechanical energy. All stored energy are thermodynamic properties.

Potential Energy (P.E.)

The Potential energy is the energy of a system due to its position or elevation with respect to some reference. Therefore, Potential energy of a mass m (kg) at height of Z (m) from a reference or datum line is

                P. E. = m Z g, where g is acceleration due to gravity m/s²).

Unit: kg-m/s_² =  N-m = J (Joule)

Kinetic Energy (K. E.)

The Energy possessed by a thermodynamic system due to its velocity is called Kinetic Energy. Kinetic energy of a mass m with a velocity of V is

                K. E. = 1/2 mv² N-m or Joule.

Internal Energy (U)

The sumtotal of random movements like translational, vibrational, and rotational energies of molecules is the kinetic energy of molecules, and it is also called the sensible energy. At higher temperatures, system will have higher sensible energy. Internal energy is associated with this motion of the molecules. It is invisible microscopic energy on the atomic and molecular level. The internal energy is an extensive property. It cannot be measured directly. Internal energy is proportional to temperature. If temperature increases, internal energy will also increase. Internal energy of a system (gas)

                U = m c_v T

                m = mass of the system (gas)

                c_v = Specific heat at constant volume

                T = Temperature in degree kelvin.

Total Energy, E = P. E. + K. E. + U

Specific energy (Energy per unit mass), e = p. e. + k. e. + u

Joule’s Law)

It states that the changes of internal energy (dU) of a perfect gas is directly proportional to the change of temperature (dT). Mathematically,

dU∝ dT or

dU = mc (T₂ – T₁)

where m is the mass of gas,

and c is the constant of proportionality, known as specific heat of a gas.

Flow Energy

Flow work and energy are seen in open, or control volume system as shown in the figure. Energy due to transfer or flow of mass across a boundary is called Flow Energy. Consider a mass (m) of fluid of specific volume v (V = m x v) enters the system at section 1-1 against a force dF (dF = dP x A). The section or layer of fluid displaces by L while doing work for continuous flow.

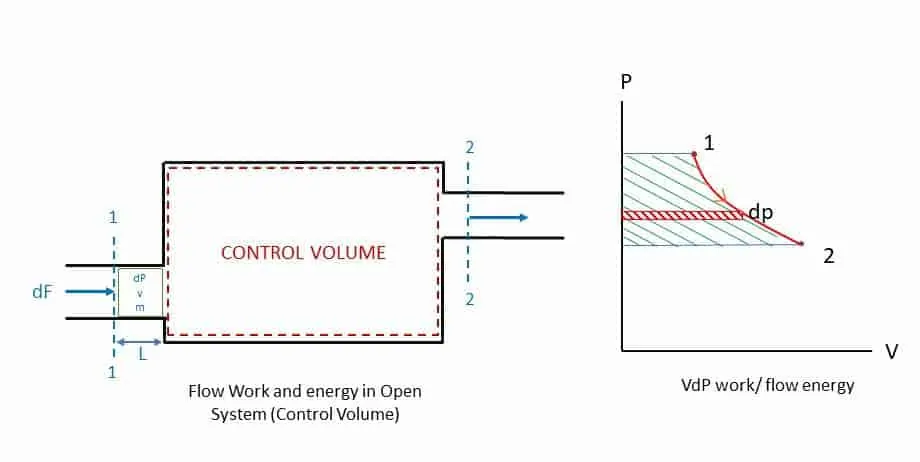
Work Done, dW = dF x L

                                = (dP x A) x L

                                = dP. (A x L)

                                = VdP

In integral form, Flow energy = ∫vdp

Heat (Q) and Work(W)

In a thermodynamic system, the concept of energy and mass transfer is very important. The energy transfer (in or out of the system) takes place through carrier of energy like Heat and Work. Heat and work are carrier of energy but not energy. Energy is a property of the system. Energy is possessed by a system.

A system does not contain heat or work. Heat and work cannot be stored but energy can be stored. Energy is property of a system. Heat and work are boundary phenomenon. They are also known as energy in transit. They can be identified only when they cross the boundary (interact with the surrounding). Heat transfer takes place because of temperature between system and the surrounding by conduction/convection/radiation. If heat transfer does not take place between the system and the surrounding, it is called adiabatic. Heat and work are measured in energy units, and they represent energy. So, heat is a form of energy that crosses boundary by virtue of temperature difference. If energy interaction is not by virtue of temperature difference in a closed system, then it is work transfer.

Both heat and work may enter the system or leave the system. They are directional quantities. Heat Transfer to a system is assigned positive sign. Heat transfer from system to surrounding is given negative sign. Work done by the system is assigned positive sign. Work done on the system is negative.

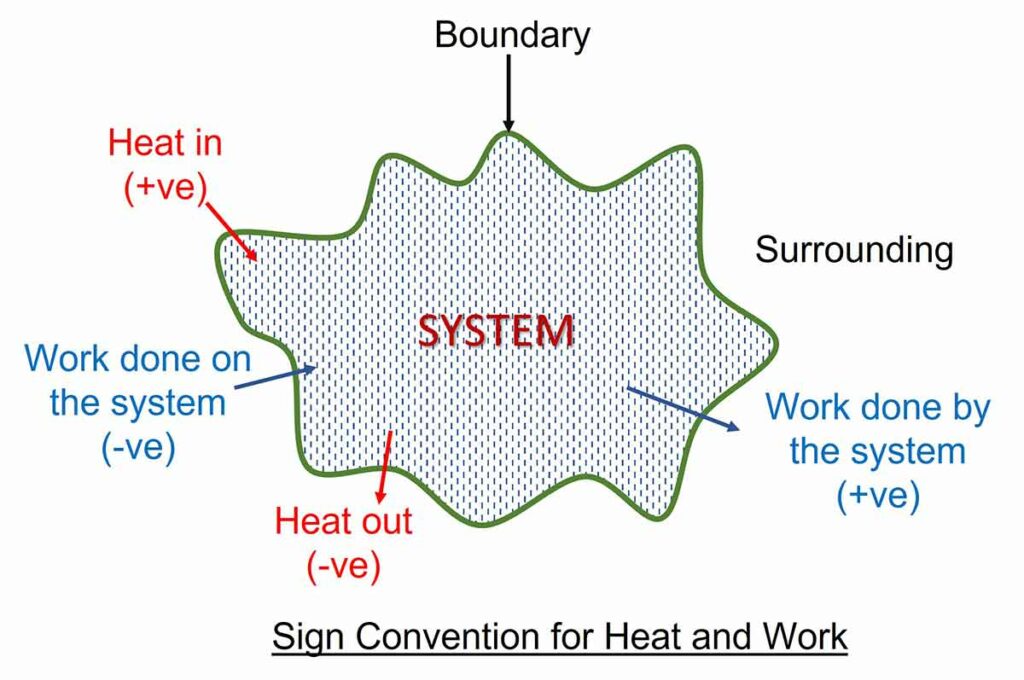
Heat is not a thermodynamic property, but temperature is a property of system. Heat represents energy and its unit is same as that of energy. Unit of heat is Joule (J) or kilojoule (kJ). The unit of rate of heat transfer is kJ/s (kW).
Heat is energy that transfer from hot body to cold body. Temperature gradient is the driving force for flow of heat.

Heat Capacity (C)

Heat Capacity of a system is the amount of heat which can change the temperature of the system by one degree.

Specific Heat or Specific Heat Capacity (c)

Specific heat or specific heat capacity is the amount of heat which can change temperature of one unit mass of a substance by one degree. If unit of heat is kJ, mass is kg and temperature is Kelvin(K); the unit od Specific heat capacity (c) will be kJ/kg K. Therefore, Heat capacity of a substance will be

                Q = m c (T₂ – T₁) kJ, Where

                                m = mass of the substance in kg,

                                c = specific heat capacity in kJ.kg K

                                T₁ = Initial temperature in kelvin

                                T₂ = Final temperature in kelvin

Solids and Liquids have only one specific heat(c). Gases have two specific heats depending on the process involved:

1. Specific heat at constant pressure (c_p)
2. Specific heat at constant volume (c_v)

Mechanical Work in thermodynamics

Thermodynamic work is energy transferred without mass transfer and not due to temperature difference with the surrounding. From mechanics we know that work is done when there is any displacement in the direction of the applied force (Work done = Force x Distance travelled). In a process of a system, work is done when there is movement of the boundary against the surrounding pressure. In thermodynamics, work transfer happens by displacement of the system boundary and such work is displacement work or boundary work (boundary phenomenon).

Let us consider a frictionless piston-cylinder arrangement as shown in the figure with a mass of air inside the cylinder. The state-1 (p₁, v₁) is in equilibrium under the action of downward force F (weight) of the piston and upward force of air inside the cylinder. Point 1 represents the state in P-V diagram.

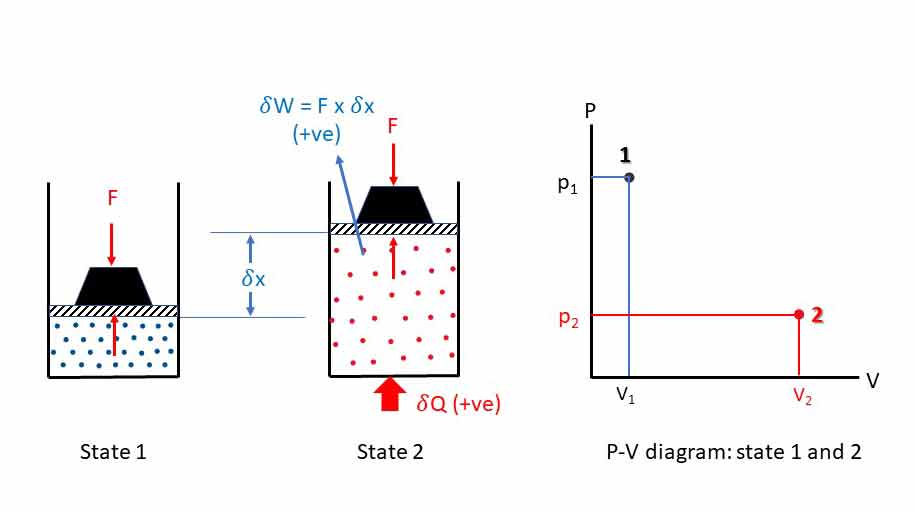
Upon adddingthe heat to the mass of air the temperature and pressure will increase. High pressure (Force = Pressure x Area) will push the piston upward by a distance x until the equilibrium at state 2 (p₂, v₂). The amount of work done is

  W = F . x

         = (p . A) . x

         = p . (A . x)

         = p V, where V is the change in volume due to expansion.

Work is done by the system on the surrounding (+ve work). This is called displacement work or boundary work. All expansion works are +ve (done by the system). If the air inside the cylinder is compressed, then work is done on the system (-ve work). This infinitesimal work is called p V work.

Path Function

Quantities whose values depend on the path followed by the thermodynamic process is called path function or process function. Both heat and work are path function. Path functions are inexact or imperfect differential. Let us understand the path function with the help of the following p-v diagram for a reversible expansion process 1-2 in a piston-cylinder arrangement. The process follows the path 1-2.

Consider a small displacement  of the piston at a pressure p. The work done for this displacement is

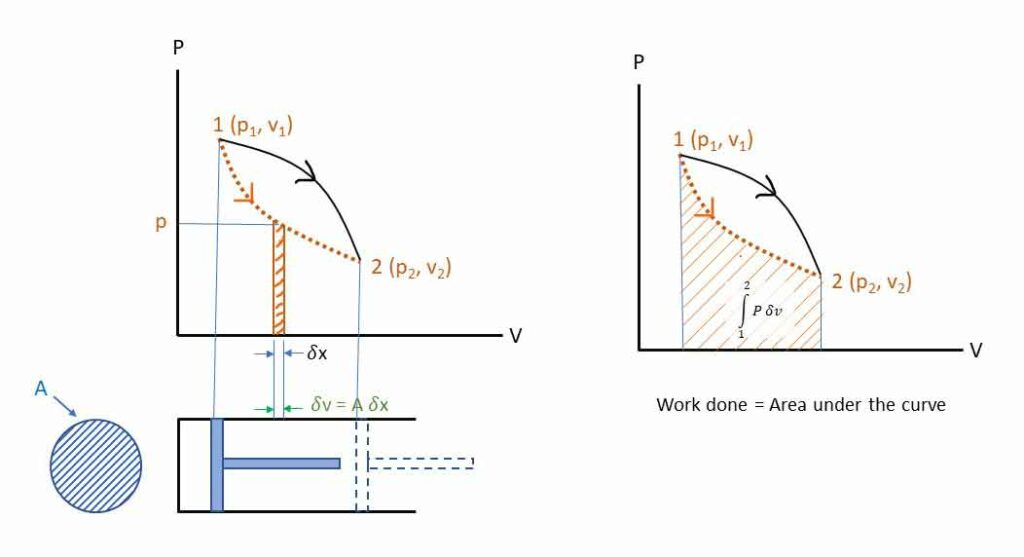
δW = F. δx = (p . A) . δx = p . (A . δx) = pδV

Total work done may be obtained by integrating from state 1 to state 2.

                ₁ W ₂ or W_1-2 = ∫p∂v

The area under the curve (p-v diagram) represents the work done during the quasistatic process 1-2. The area will be different for a different path of the process. Thus, work done is a function of the path. In other words, the amount of work done depends upon the path followed by the process (Path or process function).

Similarly, Heat transfer during a quasi-static process is also a Path or process function.

Heat transfer during a process 1-2, = ∫∂Q  = ₁ Q ₂ = Q_1-2

Point Function

Point functions or state functions are the quantities or properties of the thermodynamic system whose values are independent of the path followed by the process. Their values depend only on the state (point) of the process. All thermodynamic properties are point or state functions. In a process following the path 1-2 where volume changes from V₁ to V₂ is shown in the diagram.     ∫dv = V₂ – V₁   Value depends on the final (state) and initial (state) volume only.

Processes

We have already defined thermodynamic process in our previous post. A thermodynamic process is always associated with a change in energy and hence change in some of the properties (state) of the system. The specific condition under which the changes happen may be different. Following are the different types of thermodynamics processes:

Isobaric or Constant Pressure Process:

The pressure of the system remains constant throughout the process. Example: boiling of water in a boiler at a constant pressure. Figure represents an Isobaric process in a P-V diagram.

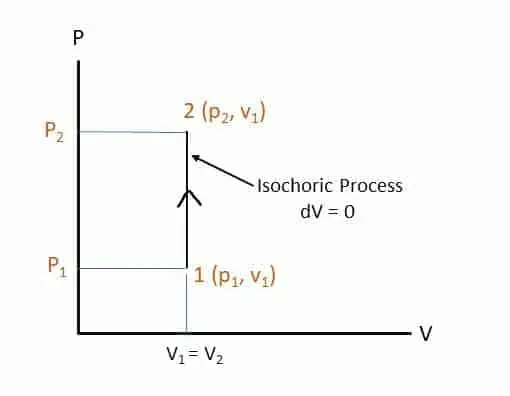
Isochoric or Constant Volume Process:

The volume of the system remains constant throughout the process. Volume at the initial state is equal to the volume at the final state of the process. Example: heating of a gas in a fixed volume (non-expanding chamber). It is also known as isovolumetric process, or isometric process. Figure represents an Isochoric process in a P-V diagram.

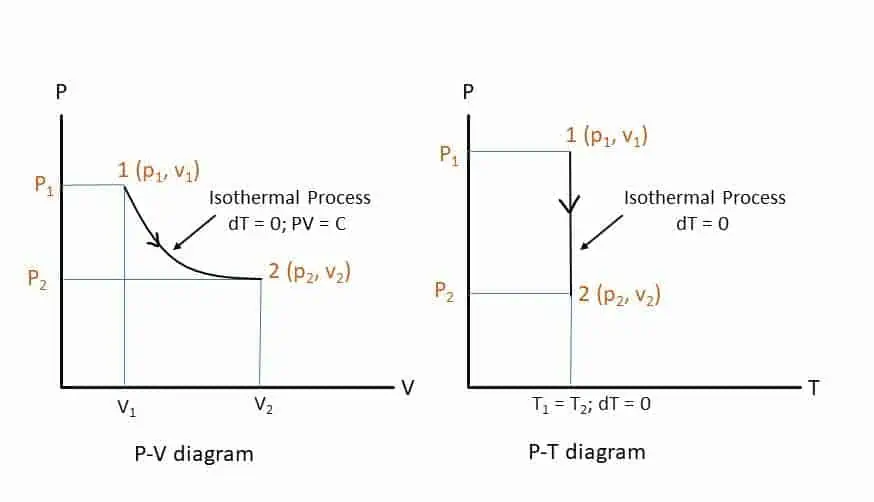
Isothermal Process or Constant pressure process:

The temperature of the system remains constant throughout the process (dT = 0). This process is governed by the Boyle’s Law and the curve is hyperbolic. The figure shows the isothermal process in P-V and P-T diagrams.

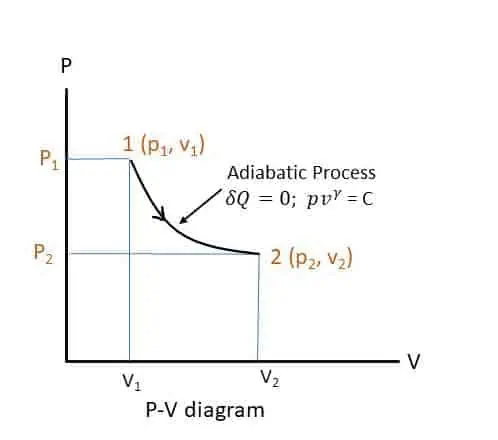
Adiabatic Process:

The system does not transfer heat with the surrounding (∂Q = 0). The Adiabatic Law is pv^ϒ = c, where ϒ is called the adiabatic index (ϒ = c_p/c_v ) and its value is 1.4 for air.

Polytropic process:

A process which obeys the law pvⁿ = c, where n is the polytropic index. The polytropic law is a generalised law for all the above processes. For n= o, p = c (isobaric process); for n =1, pv = c (isothermal process); for n = ϒ, pv^ϒ = c (adiabatic process) and for n = + ∞, v = c (isochoric process). Thus, value of polytropic index may vary from 0 to ∞.

You may watch this video for Non flow processes

Questions and Answers:

1 Compare Heat and Work in thermodynamics.

• Heat and work are boundary phenomenon i.e., they are observed when cross the boundary.
• Heat transfer is energy transfer due to temperature gradient between the system and surrounding. Work transfer is transfer of energy in a closed system not due to temperature difference.
• During thermodynamic process (change of state) heat or work transfer may take place.
• Both are path functions. Both are inexact differential (∂Q and ∂W).
• Heat and work are not thermodynamic properties of system.
• The sign convention for Heat input is positive and negative for heat rejection. Work done by the system is positive and work done by the surrounding on the system is negative.

2 Describe Specific heat of a gas.

Specific heat capacity of a gas is the amount of heat required to change the temperature of unit mass of gas (kJ/kg K). Gases have two specific heats: (i) specific heat at constant volume (c_v) and specific heat at constant pressure (c_p). The value of c_p is always greater than value of c_v.

3 Define process function and give examples.

The values of thermodynamic quantities which are function of path i.e., whose values are dependent on the path of the process are called path functions or process functions. Path function quantities are not thermodynamic properties. Heat and work are examples of path functions.

4 Give examples of state or point functions.

All thermodynamic properties like pressure, volume, temperature etc. are state or path functions. Their values depend only on the initial and final state (point) of the process.