First Laws of Thermodynamics

Zeroth Law of Thermodynamics

In this topic, we will discuss about Zeroth law and first law of thermodynamics. When two systems are at the same temperature, they will not exchange heat with each other. They are said to be in thermal equilibrium. A system is said to be in thermal equilibrium, when temperature throughout the system is same, and is equal to that of its surrounding.

Table Of Contents

Zeroth Law of Thermodynamics
First Law of Thermodynamics
- Conclusion:
LIMITATIONS OF FIRST LAW OF THERMODYNAMICS
RELATION BETWEEN TWO SPECIFIC HEATS

Zeroth Law:

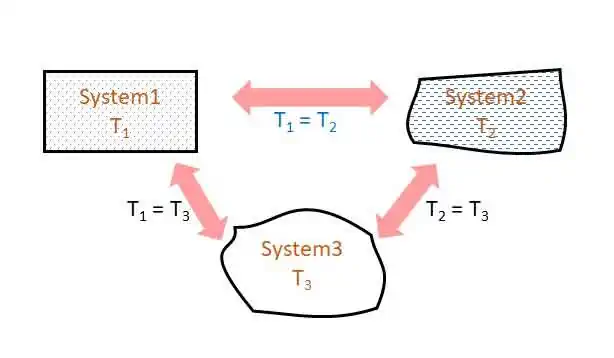
If two systems are in thermal equilibrium with a third system separately, then they are in thermal equilibrium among themselves.

Thermal equilibrium means equal temperature and there is no energy transfer due to temperature difference. If system 1 is in thermal equilibrium with system 3 and system 2 is in thermal equilibrium with system 3, then system 1 and system 2 are also in thermal equilibrium. Therefore, if T₁ = T₃ and T₂ = T₃, then T₁ = T₂ (refer the figure below). Thus, all the systems in thermal equilibrium have the same temperature, irrespective of their sizes.

Temperature

All temperature measurements are based on this Law. Temperature is one of the important properties (intensive) of a system. It is a state or point function and is a macroscopic property. If two bodies at different temperatures come in contact with each other, heat flows from the body at higher temperature to the body at lower temperature. The difference in temperature (thermal potential) is the driving agent for flow of heat energy. Temperature is be defined as the degree of hotness of a body or intensity of hotness.

Temperature measurement

A thermometer is an instrument used to measure temperature which works on the principle of zeroth law. That is why, the thermometer is brought in contact with the system, whose temperature has to be measured. High temperatures are by measured by thermocouples.

Scale of measurement

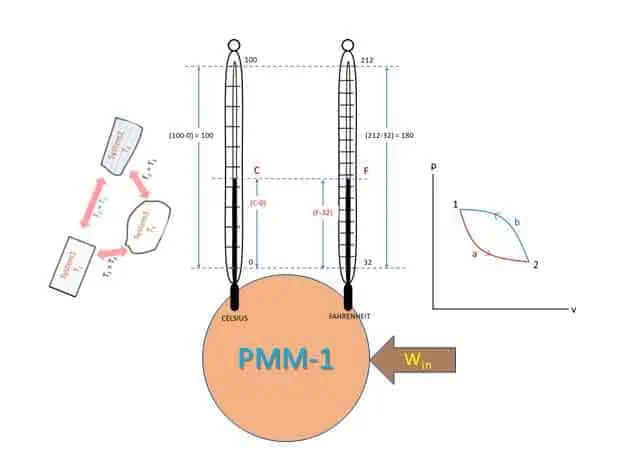
Two most used and old scales for measuring the temperature of a body are Celsius (degree centigrade) and Fahrenheit. Two fixed points are used to measure temperatures by these two scales. The linear distance between two known temperatures is divided into equal number of divisions. Temperatures of freezing and boiling water (pure water free from salt) at sea level pressure are used in this case. Thus, a linear scale is developed and is attached to the thermometer. Such scale is called empirical scale because two fixed points are assumed arbitrarily.

Celsius scale

In this scale freezing point of water (lower fixed point) is taken as 0 and boiling point of water (upper fixed point) is considered as 100. The interval between these two points is divided into 100 equal divisions and each division is called 1 degree Celsius (1 ^o C).

Fahrenheit scale

In this scale, freezing point of water is marked as 32 and boiling point of water is marked as 212. The interval is divided into 180 equal divisions and each division represents 1 degree Fahrenheit (1 ^o F).

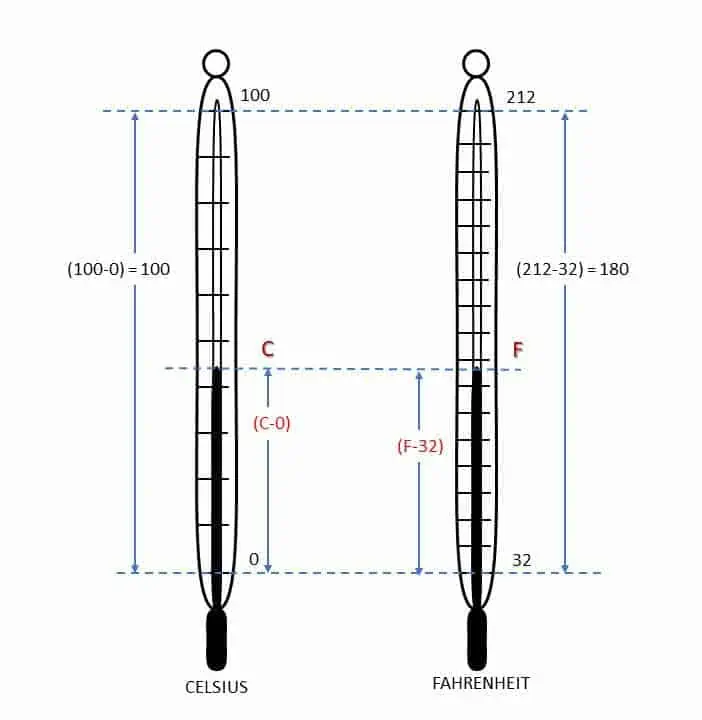
The relation between Celsius (Centigrade) and Fahrenheit scale is given by:

$\frac{C-0}{100-0} = \frac{F-32}{212-32} \rightarrow \frac{C}{5} = \frac{F-32}{9}$

Kelvin scale

In this scale of temperature, there is an absolute zero temperature below which temperatures do not exist. Absolute zero is represented by 0 K. In Celsius scale absolute zero is – 273.15 K.

Temperature in Kelvin (K) ={Temperature in Celsius (C) + 273.15} K

K = (^oC + 273.15) K

Rankine scale

This is also an absolute zero scale and is related to Fahrenheit scale. Absolute scale in Fahrenheit scale is called Rankine scale (represented by R). Absolute zero temperature is in Fahrenheit scale is -460 ^o F.

Temperature in Rankine (R) = (Temperature in Fahrenheit + 460) R

R = (^oF + 460) R

First Law of Thermodynamics

The relationship of heat and work is the basic of First Law of Thermodynamics. Heat and work are mutually convertible. It is also popularly known as law of conservation of energy. The First Law of thermodynamics can be stated in many ways.

If a closed system completes one cycle, The sum of heat interactions is equal to sum of work interactions.

$\sum{Q} = \sum{W}$

In other words: If a closed system completes one cycle the cyclic integral of heat is equal to the cyclic integral of work.

$\oint\partial Q = \oint\partial W$

$\oint\partial Q - \oint\partial W =0$

$\oint{(\partial Q} - \partial\ W) = 0$

Considering a two-process cycle shown in the p-v diagram,

Q_1-a-2 + Q_2-b-1 = W_1-a-2+ W_2-b-1

Or Q_1-a-2 – W_1-a-2 = W_2-b-1 – Q_2-b-1

This can be written in integral form:

$\int_{1}^{2}{\delta (Q-W)} = \int_{2}^{1}{\delta(W-Q)}$

$Or \int_{1}^{2}{\partial(Q-W)} = -\int_{2}^{1}{\partial(Q-W)}$

$Or\ \int_{1}^{2}{\partial(Q-W)\ }+\ \int_{2}^{1}{\partial(Q-W)} = 0$

$Or\ \int_{1}^{2}{\partial(Q-W)\ }-\ \int_{1}^{2}{\partial(Q-W)} = 0$

$Or\ \int_{1}^{2}{\partial(Q-W)\ (Path\ a)\ }=\ \int_{1}^{2}{\partial(Q-W)} (path\ b) = constant$

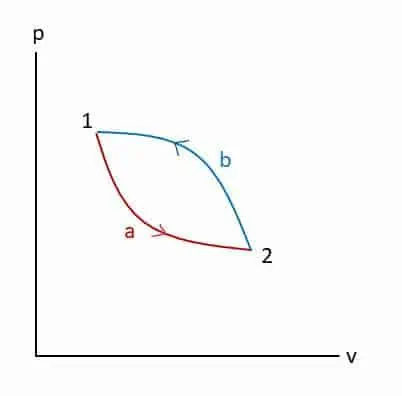
We can conclude that for any process like 1-a-2 and 1-b-2,

$\partial\ Q\ -\ \partial\ W\ =\ Constant$

$The\ difference\ (\partial\ Q\ -\ \partial\ W)\ depends\ only\ on\ the\ end\ points\ (initial\ and\ final\ state\ of\ the\ process.$

$So,\ the\ quantity\ (\partial\ Q\ -\ \partial\ W)\ is\ a\ point\ or\ state\ function\ (although\ Q\ and\ W\ are\ path\ functions).$

If that is so, for a process (1-2), difference $(\partial\ Q\ -\ \partial\ W)$ is a property of the system. This property is the Energy (E) of the system. Thus, we get another statement from the First law of thermodynamics’ statement for cyclic process.

$\partial\ Q\ -\ \partial\ W\ =\ dE \ \rightarrow(i)$

2. FIRST LAW FOR A CLOSED SYSTEM COMPLETING PROCESS (A CHANGE OF STATE)

If a system completes a process, the change in stored energy of the system is equal to the net heat interaction minus the net work interaction during the process. Mathematically,

$\partial\ Q-\partial\ W\ =\ dE$

Where, E = U (Internal energy) + PE (Potential Energy) + KE (Kinetic Energy).

For the process 1-a-2 above,

$\int_{1}^{2}{\partial(Q-W)\ }= \int_{1}^{2}dE$

Or Q_1-2 – W_1-2 = E₂ – E₁ (ii)

Q_1-2 and W_1-2 are heat transfer and work transfer during the process 1-2 respectively. E₂ and E₁ are Total energy at state 2 and 1 respectively. For the process 2-b-1 above,

$\int_{2}^{1}{\partial(Q-W)\ } = \int_{2}^{1}dE$

Or Q_2-1 – W_2-1 = E₁ – E₂

3. FIRST LAW FOR AN ISOLATED SYSTEM UNDERGOING A CHANGE OF STATE (Process)

In an isolated system No mass and energy interaction take place. Therefore,

$\partial Q\ =\ 0\ and\ \partial W\ =\ 0\ \Rightarrow\ dE\ =\ 0$

E₂ – E₁ = 0, so E₂ = E₁ = Constant (Conservation of energy)

4. A perpetual motion machine of the first kind (PMM-1) is impossible

Let us consider the two-process cycle again. Work done during the process 1 – a – 2 is area under the curve 1-a-2-4-3-1. Similarly, Work done during the process 2 – b – 1 is area under the curve 2-b-1-3-4-2.

Net Work done = Difference in area under the curve

= Area 2-b-1-3-4-2 – Area 1-a-2-4-3-1 = Area 1-a-2-b-1

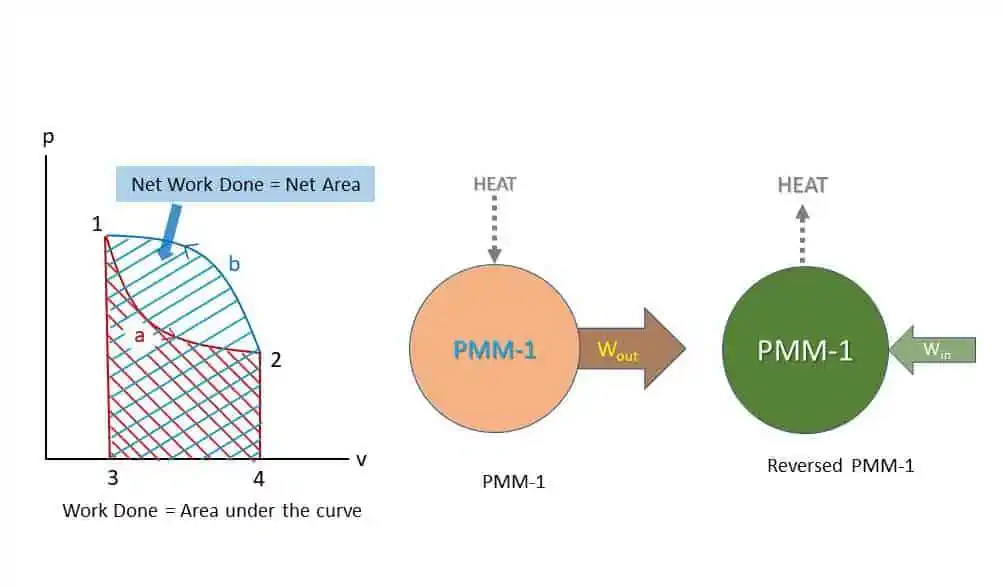
To derive this work, there must be some heat interaction (First Law of Thermodynamic). Without heat interaction work output is not possible. If there is any machine that gives work output without any heat input, such machine is called perpetual motion machine of the first kind (PMM-1) which is impossible. So PMM-1 is impossible. A perpetual motion machine of the first kind (PMM-I), is a device or machine producing a continuous supply of work without absorbing energy from the surroundings.

Conclusion:

For a process, First Law is

$\partial\ Q-\partial\ W\ =\ dE$

E is total energy and is the sum of Internal energy (U), Kinetic energy (KE) and potential energy (PE). E = U + KE + PE. If PE=0 and KE=0, First law can be written as

$\partial\ Q-\partial\ W\ =\ dU$

$\partial\ Q\ =\ dU+\partial\ W$

It is possible that Q = 0 or W = 0

We can extract Work without supplying Heat ( Q=0) at the cost of energy ( W = dU). We can supply heat to the system without doing work ( W=0) by increasing the energy of the system ( Q = dU).

LIMITATIONS OF FIRST LAW OF THERMODYNAMICS

If a closed system executes a thermodynamic cycle, the net heat transfer is equal to the net work transfer ( = ). First law of thermodynamics does not state the direction of flow of heat and work. The law does not mention any condition under which these transfers take place.
First Las states that heat and mechanical work are mutually convertible. Mechanical work can be fully converted to heat but, only a part of the heat can be converted to mechanical work. This is another limitation on conversion of one form of energy to another form.

RELATION BETWEEN TWO SPECIFIC HEATS

There are two specific heats of gas: specific heat at constant volume (c_v) and specific heat at constant pressure (c_p). From first law of thermodynamics,

$\partial Q-\partial W\ =\ dU\ \rightarrow\ (i)$

For constant pressure process,

$W_{1-2} = \int_{1}^{2}\partial W = \int_{1}^{2}\ PdV\ =\ P (V_2 - V_1)\ =\ m\ R\ (T_2 - T_1)\rightarrow\\(ii)$

From Joule’s Law,

$U2 - U1\ =\ \int_{1}^{2}dU = \int_{1}^{2}{mc_vdT}\ =\ \m\ c_v\ (T_2 - T_1)\rightarrow\\ (iii)$

From equation (i)

$Q1-2\ = \int_{1}^{2}\partial Q\ =\ m\ R\ (T_2 - T_1)\ +\ m\ c_v\ (T_2 - T_1)\ =\ m\ (T_2 - T_1)\ (R + c_v)\rightarrow\\(iv)$

But, for constant pressure process, Q_1-2 = m c_p (T₂ – T₁) (v)

From equation (iv) and (v),

m (T₂ – T₁) (R + c_v) = m c_p (T₂ – T₁)

Or R + c_v = c_p

_Or c_p– c_v = R (vi)

Dividing by c_v,

$\frac{c_p}{c_v} +1 = \frac{R}{c_v}$

Relation betweem two specific heats is

$\gamma\ +\ 1\ =\ \frac{R}{c_v}\rightarrow\\(vii)$

You can watch this video to understand the relation beween two specific heats.

We will discuss applications of First Law of Thermodynamics to Non-flow processes in the upoming blog post.

First Laws of Thermodynamics

Zeroth Law of Thermodynamics