APPLICATION OF FIRST LAW TO NON-FLOW PROCESS

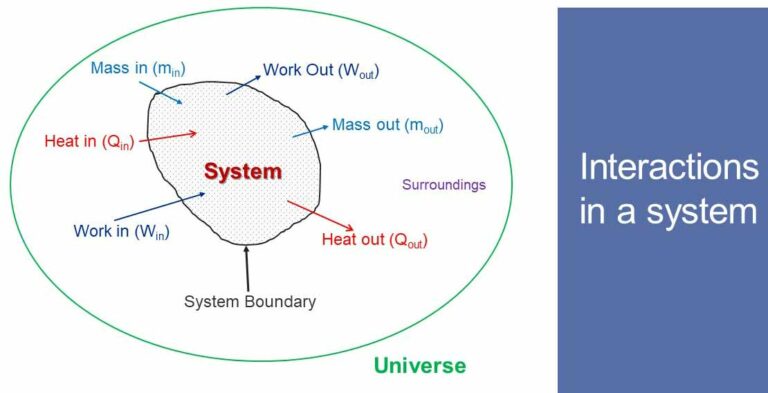
Introduction

There are two types of process in thermodynamic system.

Closed or non-flow process: This type of process happens in closed system. So, in a close system, no mass transfer takes place but, energy transfer in the form of heat and work may takes place across the boundary.
Open or flow process: This type of process occurs in open system. In open system, both mass and energy (heat and work) transfer occur. Mass enters the system and crosses the boundary after exchanging energy with the system. Flow process may be steady flow (flow through nozzle, compressor, turbine etc.) or non-steady flow (emptying or filling of a tank).

If we apply First law of thermodynamic to various non-flow processes (like isochoric, isobaric etc.), many expressions are established for work transfer, heat transfer, change in internal energy etc. Let us now discuss some of those processes:

Table Of Contents

Introduction
Reversible Constant Volume (isochoric or isometric) process:
Reversible Constant Pressure (isobaric) process:
Reversible Constant Temperature (isothermal) process:
Adiabatic (or Isentropic) Process:
RELATION BETWEEN PRESSURE, VOLUME AND TEMPERATURE DURING AN ADIABATIC PROCESS
Polytropic Process:

Reversible Constant Volume (isochoric or isometric) process:

Suppose, a gas is heated in a closed chamber so that the volume remains constant throughout the heating process. The temperature and pressure will increase as shown in P-V and P-T diagram in the figure.

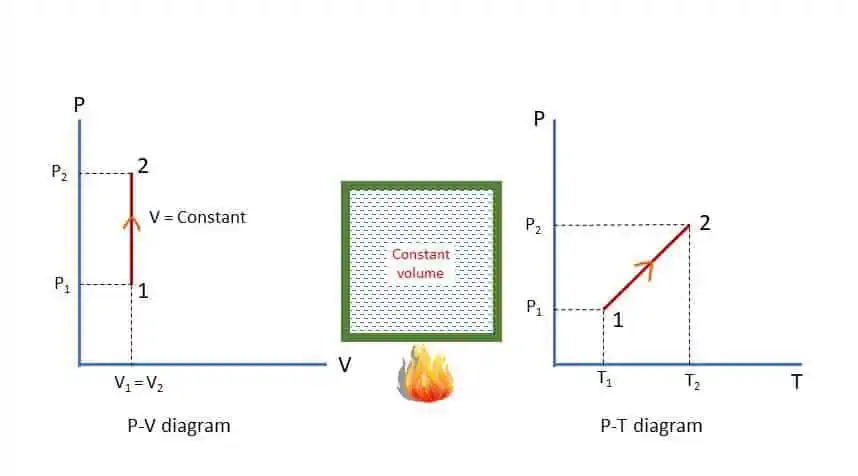
Applying First Law of Thermodynamics to the process 1-2 for ‘m’ kg of mass of gas,

$\partial\ Q\ =\ \partial\ W\ +\ dU$

Work done during isochoric process:

$\partial\ W\ =\ \int{pdv\ =\ \int{p\ .\ 0\ =\ 0},\ \ since\ dv\ =\ 0\ (Constant\ Volume\ process)}$

$Therefore,\ \partial\ Q\ =\ dU$

$\int_{1}^{2}\partial Q=\int_{1}^{2}{dU\ =\ \int_{1}^{2}{mc_vdT$

Heat Transfer in an isochoric process:

Integrating the above equation, Q_1-2 = U₂ – U₁= m c_v (T₂ – T₁) (from Joule’s Law)

Change in enthalpy in an isochoric :

Enthalpy is the sum of internal energy and product of p and v: dH = dU + d(pv)

$Integrating,\ \int_{1}^{2}{dH\ =\int_{1}^{2}dU\ +\ \int_{1}^{2}{(pv)}}$

H₂ – H₁ = (U₂ – U₁) + v (p₂ – p₁)

= (U₂ – U₁) + (p₂v₂ – p₁v₁)

= m c_v (T₂ – T₁) + m R (T₂ – T₁)

= m (T₂ – T₁) (c_v + R)

= m c_p (T₂ – T₁) (since, c_p – c_v = R)

Reversible Constant Pressure (isobaric) process:

As shown in the figure, a gas is heated in an enclosed cylinder with sliding piston with some load to produce a constant pressure p. Heating will cause increase in volume and temperature at constant pressure. If volume increases, work is done on the piston and if temperature increases, internal energy will increase (say).

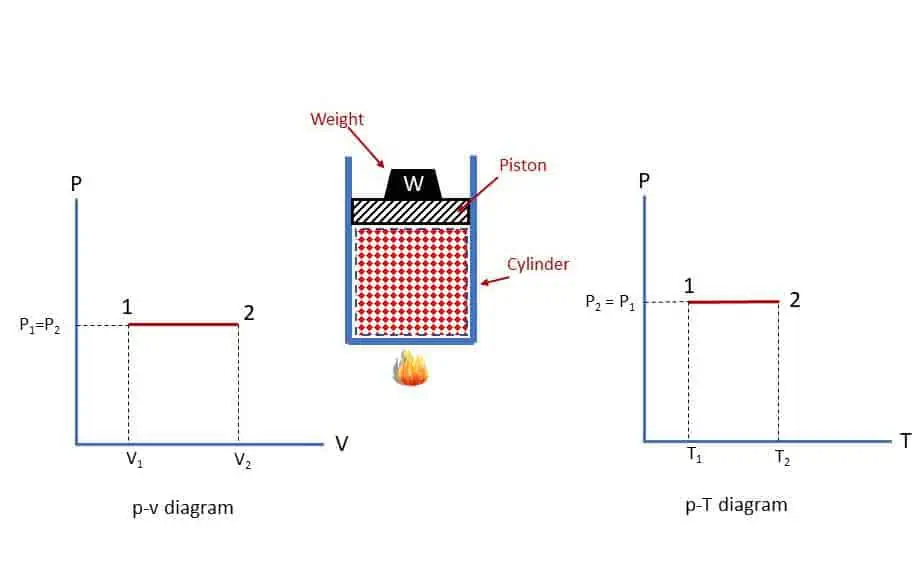
Work done by the gas during isobaric process:

$Work\ transfer,\ \partial\ W\ =pdv$

$Or,\ \int_{1}^{2}\partial W=\int_{1}^{2}pdv$

W_1-2 = p(v₂-v₁) = m R (T₂ – T₁)

Change in internal energy (isobaric process):

$From\ Joule's\ Law,\ dU\ =\ m\ c_v\ dT$

U₂ -U₁ = mc_v(T₂-T₁)

Heat Interaction (isobaric process):

$From\ First\ Law\ of\ Thermodynamics,\ \partial\ Q\ =\ \partial\ W\ +\ dU$

$Or,\ \int_{1}^{2}\partial Q=\int_{1}^{2}\partial W+\int_{1}^{2}dU$

Q_1-2 = m R (T₂ – T₁) + mc_v(T₂-T₁)

= m (R + c_v) (T₂-T₁)

= m c_p (T₂-T₁)

Thus, the heat added to the system is utilised to do mechanical work and to increase the internal energy of the system.

Change in Enthalpy in Isobaric process:

We have, dH = dU + d(pv)

$Integrating,\ \int_{1}^{2}{dH\ =\int_{1}^{2}dU\ +\ \int_{1}^{2}{(pv)}}$

H₂ – H₁ = (U₂ – U₁) + p(v₂ – v₁)

= (U₂ – U₁) + (p₂v₂ – p₁v₁)

= m c_v (T₂ – T₁) + m R (T₂ – T₁)

= m (T₂ – T₁) (c_v + R)

= m c_p (T₂ – T₁) = Q_1-2 (since c_p – c_v = R)

Reversible Constant Temperature (isothermal) process:

During an isothermal process, temperature remains contant throught the process. This process is governed by Boyle’s Law (p v = constant) and the curve is hyperbolic (as pressure in inversely proportional to volume). From Boyle’s law, p₁v₁ = p₂v₂= p v = constant

$Therefore,\ p\ =\ \frac{p_1v_1}{v}\rightarrow (i)$

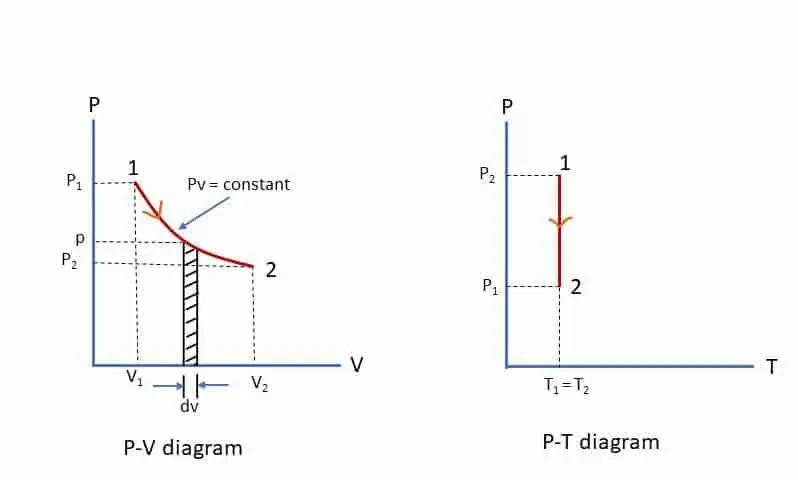
Isothermal or Constant temperature process p-v and p-T diagram

Work done by the gas during the process 1-2:

$\int_{1}^{2}\partial W=\int_{1}^{2}pdv$

$Or,\ W_{1-2}=\int_{1}^{2}{\frac{p_1v_1}{v}dv}$

$=\ p_1v_1\int_{1}^{2}{\frac{1}{v}dv}$

$\ =p_1v_1\left[log_ev\right]_1^2$

$=\ p_1v_1\left(\log_e{v_2}-\log_e{v_1}\right)$

$=p_1v_1\ \log_e{\frac{v_2}{v_1}}$

$=2.3p_1v_1\log{\frac{v_2}{v_1}}$

$=2.3p_1v_1\log{r_e}$

$Where,\ r_e = \frac{v_2}{v_1}= Expansion\ ratio$

For compression process, Work done by the system,

$=2.3p_1v_1\log{\frac{v_1}{v_2}}$

$=2.3p_1v_1\log{r_c}$

$Where,\ r_c = \frac{v_1}{v_2}= Compresion\ ratio$

Change in internal energy (isothermal process):

For isothermal process, T₁ = T₂, there is no change in internal energy as the change in temperature is zero.

U₂ – U₁ = m c_v (T₂ – T₁) = 0

Heat transferred (isothermal process):

From first law of thermodynamics,

$\partial\ Q\ =\ \partial\ W\ +\ dU$

Q_1-2 = W_1-2 + 0 = W_1-2

$\ =2.3p_1v_1\log{r_e}$

In an isothermal process, all the heat supplied to the system is used to do mechanical work.

Change in enthalpy (isothermal):

H₂ – H₁ = m c_p (T₂ – T₁) = 0 (since T₂ = T₁); Enthalpy remains same.

Consider watching this video on Isobaric and isothermal processes:

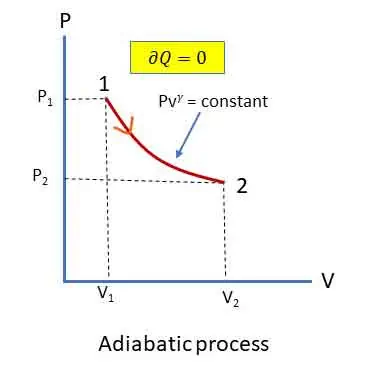
Adiabatic (or Isentropic) Process:

In this process, no heat transfer takes place (Q = 0). Reversible adiabatic processes are frictionless and are called isentropic process.

From First law of thermodynamics,

$\partial\ Q\ =\ \partial\ W\ +\ dU$

$0=\ \partial W\ +\ dU$

$Or,\ pdv+mc_vdT=0$

$Or,\ dT=-\frac{pdv}{mc_v}\rightarrow(i)$

Isentropic process p-v diagram — Isentropic process

From gas equation, pv = m R T

Differentiating both sides,

Pdv + vdp = m R dT

$dT=\frac{pdv+vdp}{mR}\rightarrow \ (ii)$

Equating equations (i) and (ii)

$-\frac{pdv}{mc_v}=\frac{pdv+vdp}{mR}$

$pdv\ +\ vdp=-\frac{pdv}{mc_v}.mR$

$pdv\ +\ vdp=-\frac{pdv}{c_v}.(c_p-c_v)$

$\frac{pdv+vdp}{pdv}=-\gamma+1$

$1+\frac{v}{dv}\frac{dp}{p}=-\gamma+1$

$\gamma=-\frac{v}{dv}\frac{dp}{p}$

$\gamma\frac{dv}{v}=-\frac{dp}{p}$

Integrating both sides of the equation,

$\int{\gamma\frac{dv}{v}=-\int\frac{dp}{p}}$

$\gamma\log_e{v\ =\ -\log_e{p\ +\log_e{C}}}$

$\log_e{p\ +\ \gamma\ \log_e{v\ =\ \log_e{C}}}$

$\log_e{pv^\gamma=\log_e{C}}$

$pv^\gamma=C$

Equation (iii) is the equation (or law) for reversible adiabatic or isentropic process.

Work done during an isentropic process:

$\partial\ W\ =\ pdv\rightarrow\ (iv)$

From adiabatic law {equation (iii)},

$pv^\gamma=p_1v_1^\gamma$

$p=\frac{p_1v_1^\gamma}{v^\gamma}=p_1v_1^{\gamma}v^{-\gamma}$

Putting the value of p in the equation (iv)

$\partial W=p_1v_1^\gamma v^{-\gamma}dv$

Integrating from 1 to 2 on both sides of the equation,

$W_{1-2}=p_1v_1^\gamma\left[\frac{v^{-\gamma+1}}{-\gamma+1}\right]_1^2$

$W_{1-2}=\frac{p_1v_1^\gamma}{-\gamma+1}\left[v_2^{1-\gamma}-v_1^{1-\gamma}\right]$

$W_{1-2}=\frac{p_2v_2^\gamma v_2^{1-\gamma}-p_1v_1^\gamma v_1^{1-\gamma}}{1-\gamma}$

$Since,\ p_1v_1^\gamma=\ p_2v_2^\gamma$

$W_{1-2}=\frac{p_2v_2-p_1v_1}{\left(1-\gamma\right)}$

$W_{1-2}=\frac{p_1v_1-p_2v_2}{\gamma-\ 1}$

$W_{1-2}=\frac{mR\left(T_1-T_2\right)}{\gamma-1}$

Change in internal energy during an isentropic process:

Change in internal energy is always: U₂ – U₁ = m c_v (T₂-T₁)

Heat transfer during an isentropic process:

There is no heat transfer in adiabatic process, So, Q_1-2 = 0

Change in enthalpy during an isentropic process:

dH = dU + d(pv)

$\int_{1}^{2}{dH\ =\int_{1}^{2}dU\ +\ \int_{1}^{2}\left(pv\right)}$

H₂ – H₁ = (U₂ – U₁) + p(v₂ – v₁)

= (U₂ – U₁) + (p₂v₂ – p₁v₁)

= m c_v (T₂ – T₁) + m R (T₂ – T₁)

= m (T₂ – T₁) (c_v + R)

= m c_p (T₂ – T₁) = Q_1-2 since (c_p – c_v = R)

You may watch this video on Adiabatic process:

RELATION BETWEEN PRESSURE, VOLUME AND TEMPERATURE DURING AN ADIABATIC PROCESS

The Adiabatic law is

$p_1v_1^\gamma=p_2v_2^\gamma$

$Or\ \frac{p_1}{p_2}=\left(\frac{v_2}{v_1}\right)^\gamma$

$Or\frac{v_1}{v_2}=\left(\frac{p_2}{p_1}\right)^\frac{1}{\gamma}\rightarrow\left(i\right)$

$From\ gas\ equation,\ \frac{p_1v_1}{T_1}=\frac{p_2v_2}{T_2}$

$Or\ \frac{v_1}{v_2}=\frac{p_2T_1}{p_1T_2}\rightarrow\left(ii\right)$

$From\ equation\ \left(i\right)\ and\ \left(ii\right)\thinsp\frac{p_2T_1}{p_1T_2}=\left(\frac{p_2}{p_1}\right)^\frac{1}{\gamma}$

$Or\ \frac{T_2}{T_1}=\left(\frac{p_2}{p_1}\right)^\frac{\gamma-1}{\gamma}\rightarrow\left(iii\right)$

Similarly, we can establish the relation between Temperature and volume:

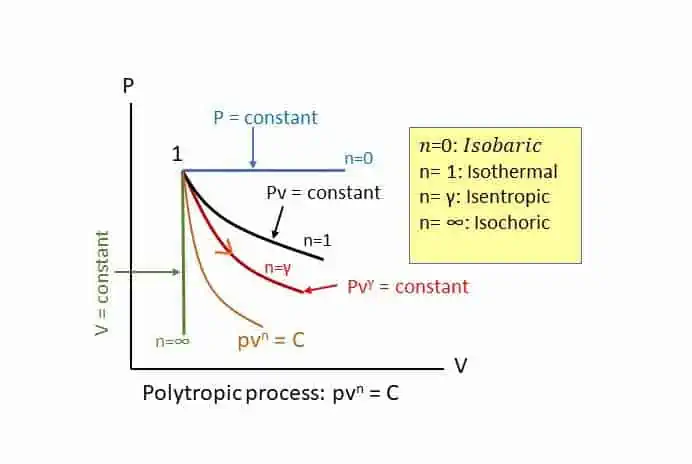
$\frac{T_2}{T_1}=\left(\frac{v_1}{v_2}\right)^{\gamma-1}\rightarrow\left(iv\right)$

Polytropic Process:

Polytropic process is the general process with polytropic index of n in the equation:

$pv^n = Constant$

The value of n may vary from Zero to infinity. The following figure is self-explanatory for the general nature of the Polytropic process.

APPLICATION OF FIRST LAW TO NON-FLOW PROCESS

Introduction